En el amplio y diverso mundo de las matemáticas, el número pi (π) es una de las cifras que más ha llamado la atención, siendo objeto de estudio a lo largo de los siglos. Este número, equivalente al aproximado de 3,1416, tiene un gran impacto en la actualidad.
Tal es la significancia de pi que, incluso, se celebra el denominado Día de Pi (π) a nivel internacional cada 14 de marzo. ¿Por qué? Te contamos más de esta increíble cifra a continuación.
Todo sobre pi (π)

¿Qué es pi (π)?
El número π (pi) se define, en geometría euclidiana, como la relación entre la longitud de una circunferencia y su diámetro.
Generalmente redondeado como 3.14, pi (π) es un número irracional, lo que quiere decir que tiene decimales infinitos y no periódicos, razón por la que no se puede expresar como una fracción. Esto también implica que nunca podremos encontrar todos los números de pi.
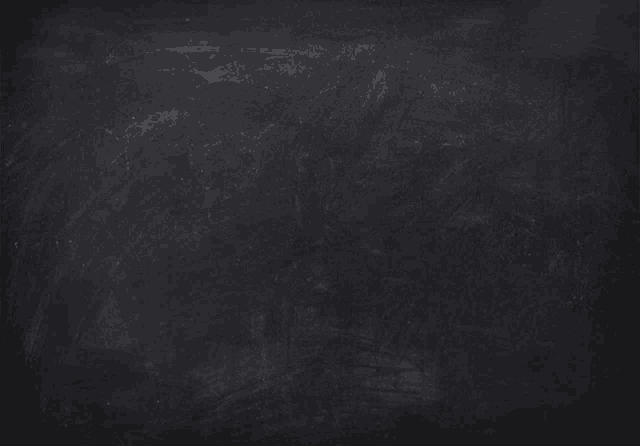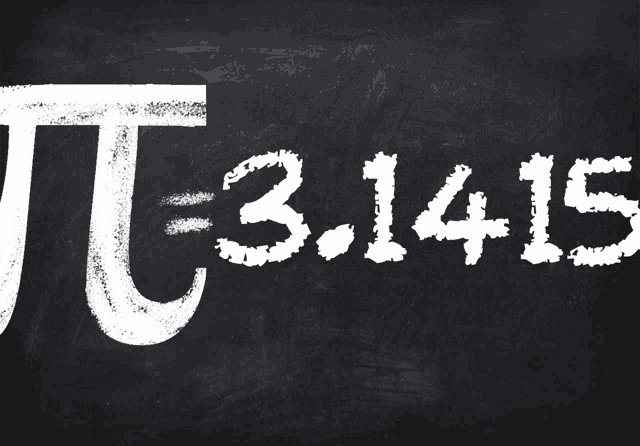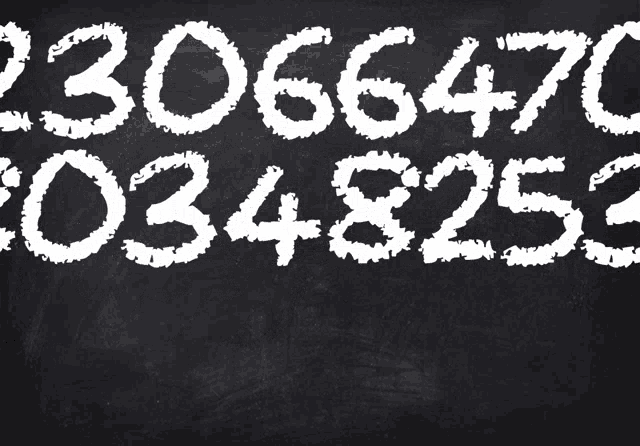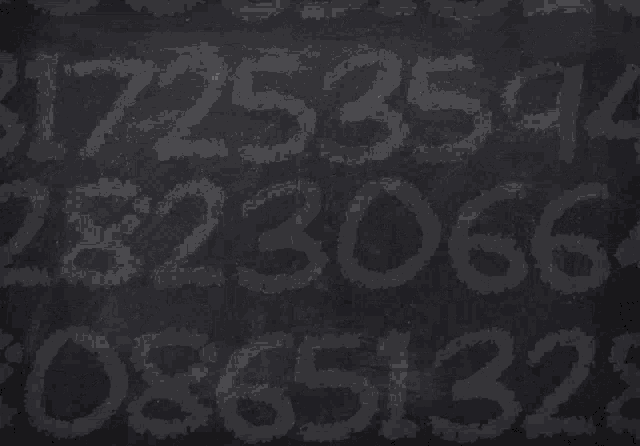
No obstante, a lo largo de la historia, los matemáticos siempre han hecho intentos por descubrir la mayor cantidad de dígitos de pi posibles. Un ejemplo es que, en 2022, Google rompió un récord mundial luego de calcular 100 billones de dígitos de pi.
Probablemente hayas escuchado mucho de pi, y es que este número irracional no solo es fundamental en la geometría y en otras ramas de las matemáticas, sino que también se aplica en la física, la ingeniería y la tecnología, entre otras áreas.
LEE TAMBIÉN
- ¿Qué significa UwU?
- Pez remo: qué es y por qué se cree que predice sismos
- ¿Qué significa el martes 13?
En fácil: ¿cómo se calcula pi (π)?
Para muchas personas, las matemáticas no son algo fácil, así que a continuación te ayudamos a entender de forma rápida lo que es el número pi (π).
En simples palabras, pi (π) es el número de veces que cabe el diámetro de un círculo en su circunferencia.
Es decir, si divides la circunferencia por el diámetro de un círculo, te resultará 3,1415926... o sea, pi (π).
¿Por qué se le llama pi (π)?
El término "pi" proviene de la letra griega π (pi), que es la primera letra del término griego "periferia" o "perímetro".
Este número irracional fue denominado como pi (π) por primera vez por el matemático británico William Oughtred (1574-1660), quien introdujo el símbolo "x" para la multiplicación y también las abreviaturas de "sin" y "cos" para seno y coseno. No obstante, fue popularizado por el matemático suizo Leonhard Euler (1707-1783).
¿Por qué se celebra el Día de Pi (π)?
La derivación de los primeros números de pi (3,14) fueron los que llevaron al físico estadounidense Larry Shaw a proponer en el año 1988 el 14 de marzo como el Día de π (pi), el que además puede celebrarse incluso con más exactitud a la 1:59 a. m. o p. m., para poder llegar a sus primeros seis números 3,14159.
Hoy en día, esta fecha es aceptada en todo el mundo como un espacio para celebrar las matemáticas y ver su valor en la construcción de nuestra sociedad y en nuestro día a día.

El Día de Pi (π) para festejar las matemáticas
La matemática es la base de la comprensión y resolución de problemas en una variedad de disciplinas, y su impacto se extiende a todas las esferas de nuestra existencia diaria. Como calcular gastos en el supermercado hasta diseñar planes financieros, desde la programación de rutas en el tráfico hasta la elaboración de recetas culinarias.
Cristian Gúmera, Director de Productos de Santillana Chile, hizo un llamado a reflexionar sobre el impacto positivo de las matemáticas en el Día de π (pi).
"Veamos este día como una oportunidad para reconocer y apreciar la importancia de cultivar habilidades matemáticas en el ámbito educativo y en la sociedad en general”, añadiendo que, “la educación matemática no sólo es un requisito académico, también es un habilitador clave para el desarrollo personal y profesional. Al fomentar el estudio de la matemática, estamos equipando a las generaciones futuras con las herramientas necesarias para enfrentar los desafíos del mundo moderno de manera informada y creativa".

Físicos encuentran una nueva forma de representar el número pi
Científicos del Instituto Indio de Ciencias (IISc) encontraron una nueva representación en serie para el número pi, según se conoció en junio de este 2024. Esta proporciona una forma más sencilla de extraer pi de los cálculos implicados en procesos de desciframiento, como la dispersión cuántica de partículas de alta energía.
La nueva fórmula bajo un cierto límite se acerca mucho a la representación de pi sugerida por el matemático indio Sangamagrama Madhava en el siglo XV, que fue la primera serie para pi registrada en la historia.
El estudio fue realizado por Arnab Saha, un posdoctorado y Aninda Sinha, profesora del Centro de Física de Altas Energías (CHEP), y ha sido publicado en Physical Review Letters.
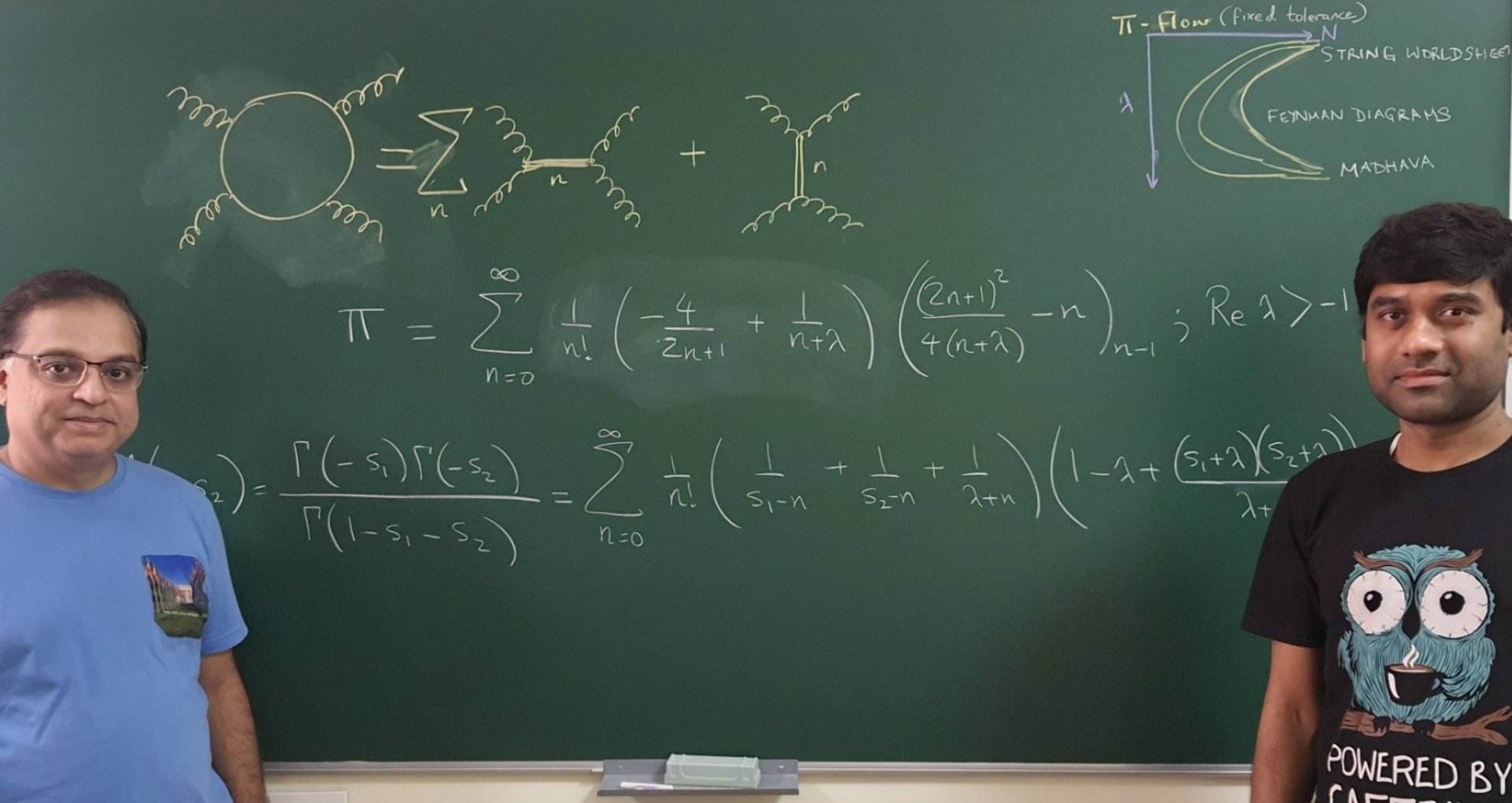
"Al principio, nuestros esfuerzos no se dirigieron a encontrar una forma de analizar pi. Todo lo que hacíamos era estudiar la física de alta energía en la teoría cuántica e intentar desarrollar un modelo con menos parámetros y más precisos para entender cómo interactúan las partículas. Nos emocionamos cuando encontramos una nueva forma de analizar pi", afirma Sinha.
El grupo de Sinha está interesado en la teoría de cuerdas, el marco teórico que presupone que todos los procesos cuánticos de la naturaleza simplemente utilizan diferentes modos de vibración pulsados en una cuerda.
Modelar estos procesos no es fácil, porque hay varios parámetros que deben tenerse en cuenta para cada partícula en movimiento. Saha, que ha estado trabajando en el problema de optimización, buscaba formas de representar de manera eficiente estas interacciones de partículas. Para desarrollar un modelo eficiente, él y Sinha decidieron combinar dos herramientas matemáticas: la función Euler-Beta y el diagrama de Feynman.
Lo que el equipo encontró no fue solo un modelo eficiente que podría explicar la interacción de partículas, sino también una representación en serie de pi. En matemáticas, una serie se utiliza para representar un parámetro como "p" en su forma de componente. Si pi es el "plato", entonces la serie es la "receta". pi se puede representar como una combinación de muchos números de parámetros (o ingredientes).
Encontrar el número y la combinación correctos de estos parámetros para acercarse rápidamente al valor exacto de pi ha sido un desafío. La serie con la que se han topado Sinha y Saha combina parámetros específicos de tal manera que los científicos pueden llegar rápidamente al valor de pi, que luego puede incorporarse en cálculos, como los que se utilizan para descifrar la dispersión de partículas de alta energía.
"Los físicos (y los matemáticos) no han logrado esto hasta ahora porque no tenían las herramientas adecuadas, que solo se encontraron gracias al trabajo que hemos estado haciendo con colaboradores durante los últimos tres años aproximadamente", explica Sinha. "A principios de los años 70, los científicos examinaron brevemente esta línea de investigación, pero la abandonaron rápidamente porque era demasiado complicada".
"Hacer este tipo de trabajo, aunque no tenga una aplicación inmediata en la vida diaria, proporciona el puro placer de hacer teoría por el simple hecho de hacerla", añade Sinha.
Los primeros mil números de pi (π)
Como te comentamos anteriormente, el valor con el que conocemos a pi es de 3.14. No obstante, en seguida te presentamos los primeros mil números de pi, dispuestos en grupos de 50 dígitos:
3.14159265358979323846264338327950288419716939937510
58209749445923078164062862089986280348253421170679
82148086513282306647093844609550582231725359408128
48111745028410270193852110555964462294895493038196
44288109756659334461284756482337867831652712019091
45648566923460348610454326648213393607260249141273
72458700660631558817488152092096282925409171536436
78925903600113305305488204665213841469519415116094
33057270365759591953092186117381932611793105118548
07446237996274956735188575272489122793818301194912
98336733624406566430860213949463952247371907021798
60943702770539217176293176752384674818467669405132
00056812714526356082778577134275778960917363717872
14684409012249534301465495853710507922796892589235
42019956112129021960864034418159813629774771309960
51870721134999999837297804995105973173281609631859
50244594553469083026425223082533446850352619311881
71010003137838752886587533208381420617177669147303
59825349042875546873115956286388235378759375195778
18577805321712268066130019278766111959092164201989




